数学是一门深奥的学科，而集合论作为其中最基础的分支之一，扮演着非常重要的角色。康托尔创造了现代集合论的思想体系，并提出了无穷集合的基数概念，但同时也引发了一系列漏洞和反常现象。希尔伯特提出了形式化集合论，并引入了选择公理等一系列概念和定理，构建了一种更加完善、系统的集合论体系。本文将对集合论的基本概念、康托尔集合论的发展、局限性和希尔伯特的集合论理论进行阐释，希望能够帮助读者更好地理解这一基础学科，从而对数学有更深入的认识。

在数学领域的发展史上，康托尔和希尔伯特之争是一段颇具代表性的历史争议。这场争议的焦点是集合论的理论与应用。

希尔伯特

一、集合论的基本概念

集合论是现代数学中的一门重要学科，涉及到集合及其性质的研究。集合是由某些对象组成的总体，每个对象称为集合元素。集合的基本概念有：子集、并集、交集、差集等。

以集合A={1, 2, 3}、集合B={2, 3, 4}为例，集合A与集合B的交集为{2, 3}，并集为{1, 2, 3, 4}，差集为{1}。

为了更好地理解什么是集合，我们可以以实际生活中的例子作为参考，例如：一支笔、一张纸、一部手机这些物品可以构成三个不同的集合。集合的元素可以是任意类型的对象，例如数字、字母、图形、函数等。

二、康托尔集合论的发展

康托尔是集合论的创始人，他的理论对现代数学的发展有着深远的影响。康托尔提出了实数连续统假设、对等原则、基数概念等核心概念，创建了现代集合论的体系。

康托尔

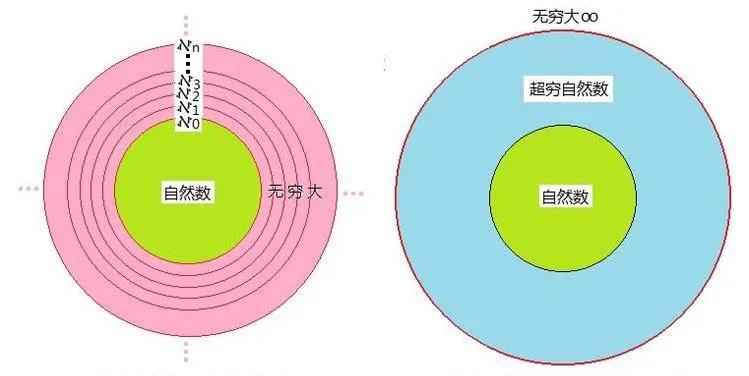
实数连续统假设指的是，在实数区间上不存在介于可数集合和连续集合之间的集合。对等原则指的是，如果两个集合可以一一对应，则两个集合具有相同的基数。基数概念指的是集合中元素的数量或大小，比如可数集合、不可数集合等。

康托尔在研究无穷集合时，提出了令人惊奇的结论：有些无穷集合的基数比其他无穷集合的基数大。这种“无穷多种大小”的概念引起了当时数学家们广泛关注。

三、康托尔理论的局限性

然而，随着康托尔理论的深入研究，一些问题开始浮现。康托尔创造的集合论体系存在着许多悖论和不合逻辑的地方，受到了严格的质疑。其中最著名的就是康托尔的悖论：集合论的一个集合不能包括自己这个元素，但可能包含其他的集合。这一悖论直接挑战了康托尔的理论体系，导致他的理论陷入了困境。

另外一个重要问题是实数连续统假设，虽然康托尔在一些特殊情况下证明了其的正确性，但是至今仍无法完全解决该问题。

康托尔理论的局限性迫使数学家们不断探索新的集合论体系，以期能克服康托尔理论的局限性。

四、希尔伯特的集合论理论

希尔伯特是当时数学领域中的权威人物，他认为康托尔理论存在一些漏洞和缺陷，并提出了自己的集合论理论，试图解决集合论中的问题。

希尔伯特的集合论理论被称为“形式化集合论”，其核心是选择公理，该公理表述了在无穷多个集合中进行选取的过程，是希尔伯特研究无穷集合的关键。希尔伯特的选择公理确保了集合的存在性、确定性和有限性，从而避免了康托尔理论中的一些漏洞和悖论。

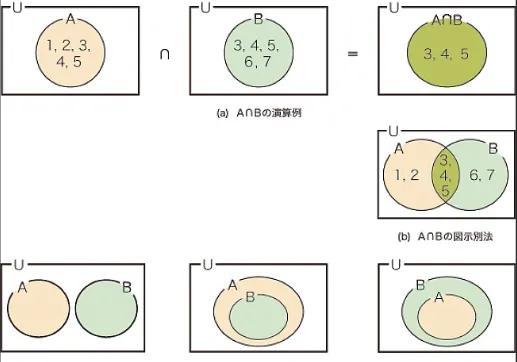
形式化集合论示例

除了选择公理之外，希尔伯特还提出了可数性定理、极大原理、良构定理等一系列定理和概念，为现代集合论的发展奠定了基础。

五、结语

康托尔与希尔伯特之争对现代数学的发展产生了深远的影响。虽然康托尔的理论受到了很多批评和质疑，但是他创造的集合论体系为现代数学的发展开创了先河。而希尔伯特的形式化集合论则为数学家们提供了一个新的方法和思路，用来解决集合论中存在的问题，并且成为现代数学的一个重要分支。